Statistics
Autocorrelation
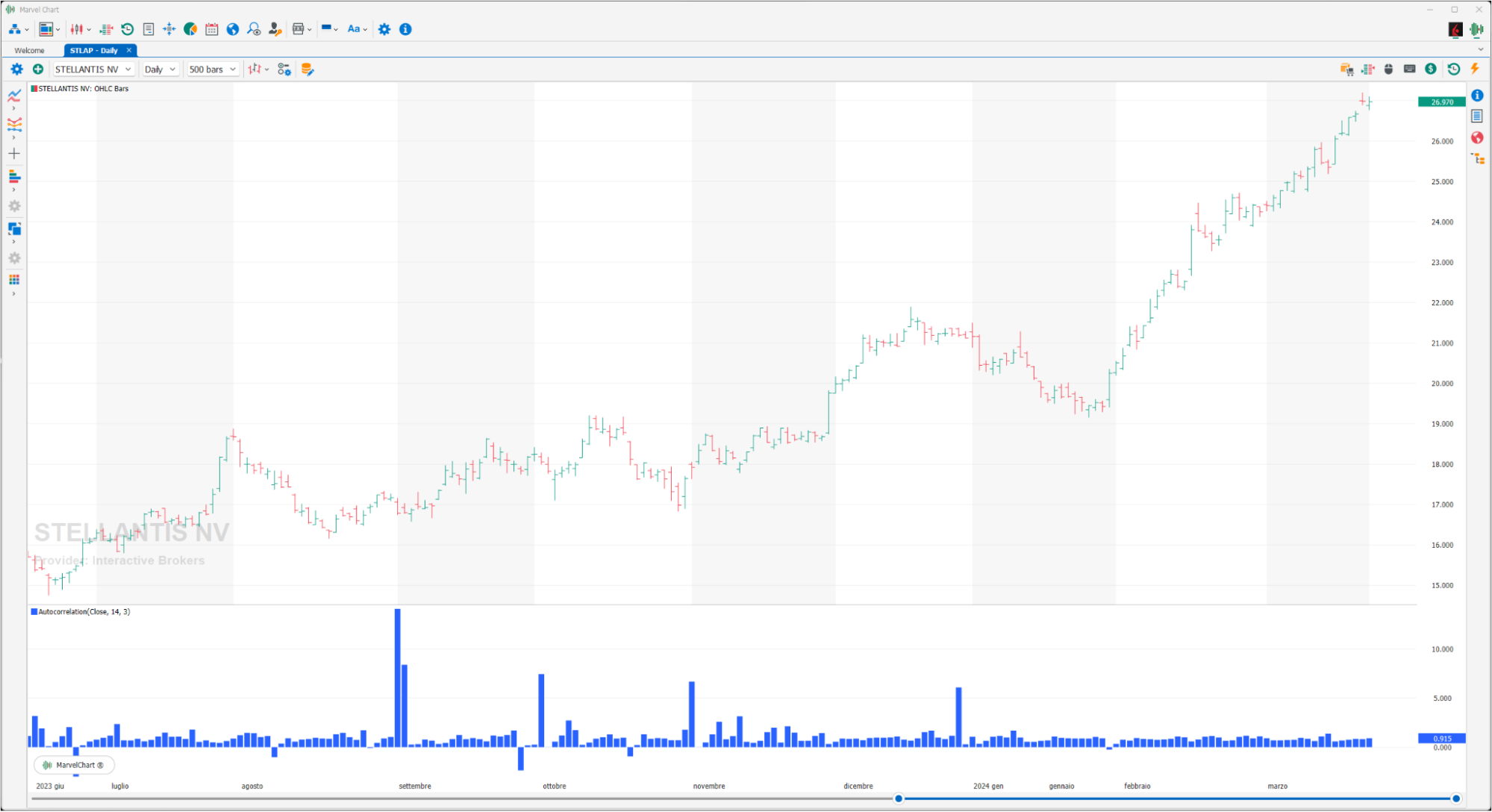
Autocorrelation is the correlation of a signal with a time-delayed copy of itself. Basically, it is the similarity between the values of a random variable as a function of their time lag. Autocorrelation analysis is a mathematical tool for finding repetitive patterns, such as the presence of a periodic signal obscured by noise, or identifying the missing fundamental frequency in a signal implied by its harmonic frequencies. It is often used in signal processing to analyze functions or series of values, such as signals over time.
Chande Forecast Oscillator
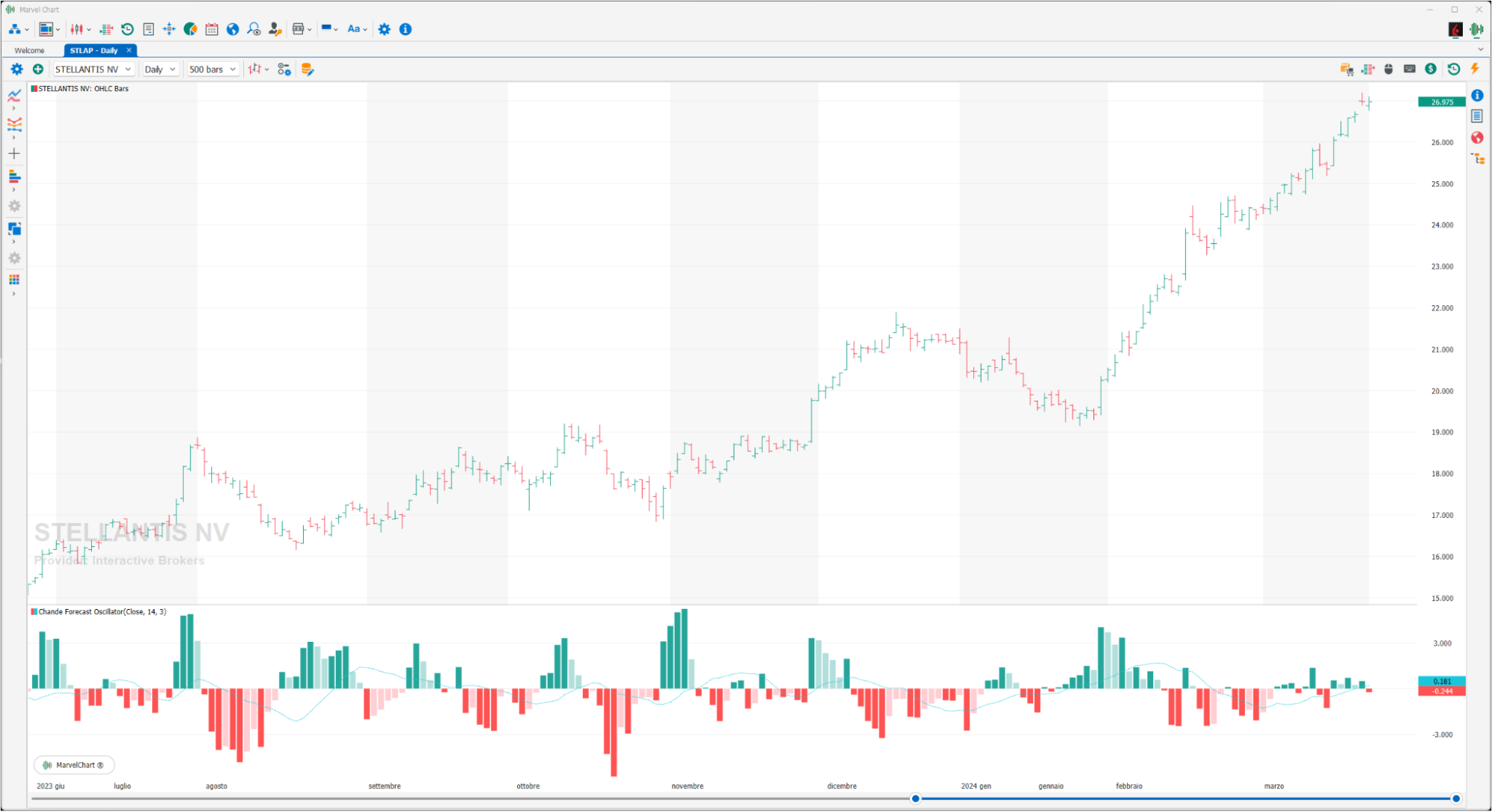
The Chande Forecast Oscillator is an indicator based on linear regression: it plots the percentage difference between the expected price, through linear regression, and the current price. When the oscillator is greater than zero, the expected price is higher than the current price, otherwise the indicator assumes negative values. Therefore, if the indicator is greater than zero, the presence of an uptrend is assumed, while when the indicator is less than zero, a downtrend is expected. Its creator, Tushar Chande, suggests plotting an x-period moving average of the indicator: in this way, BUY and SELL signals are obtained with the crossing, upwards or downwards, between the indicator and its moving average.
Change %
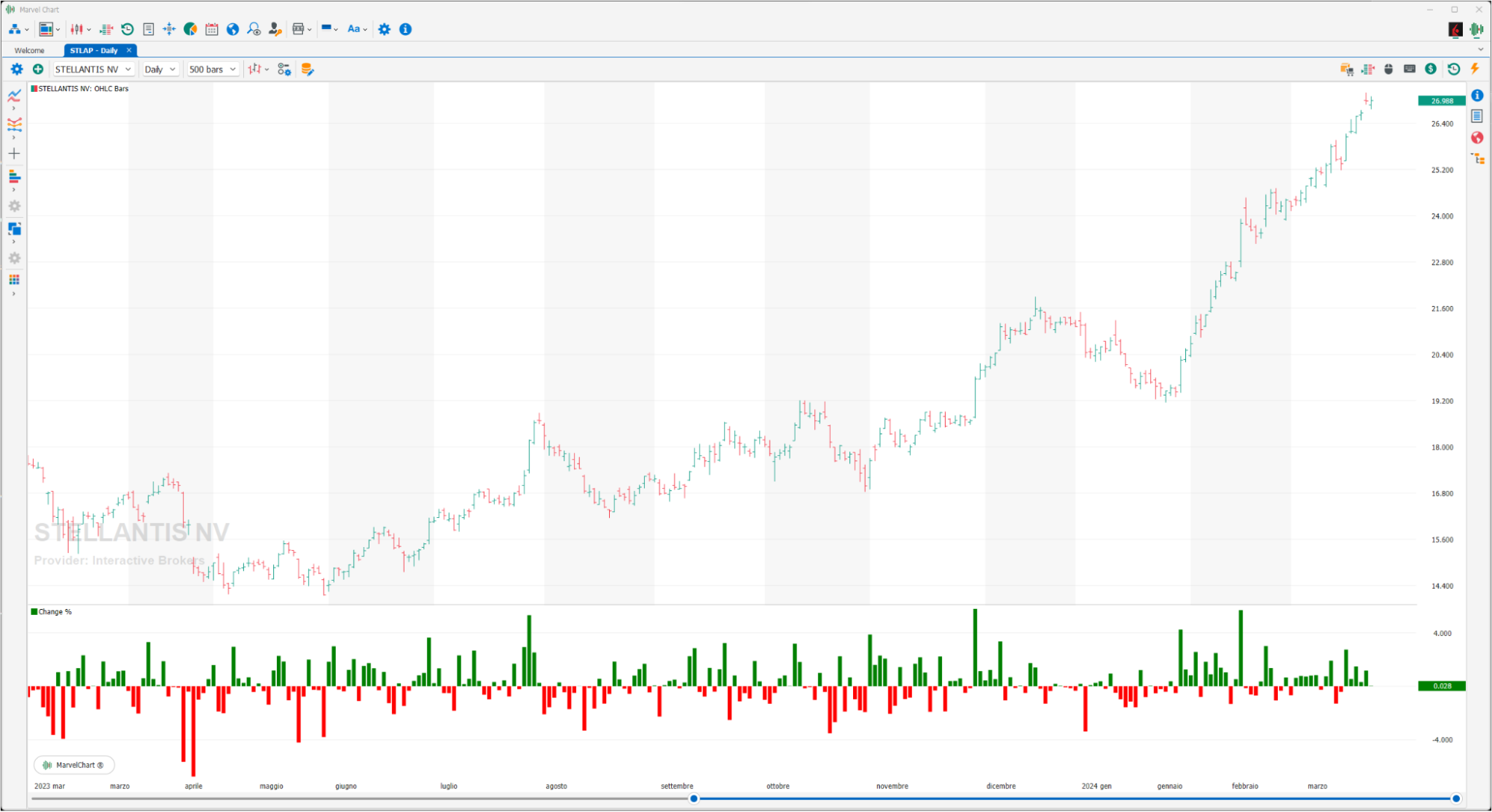
Change % is a simple statistical indicator: it displays the % change of financial instruments compared to the CLOSE of the previous day. It is not influenced by the selected timeframe because it does not take the CLOSE of the previous bar as a reference, but that of the previous day.
Generic Oscillator
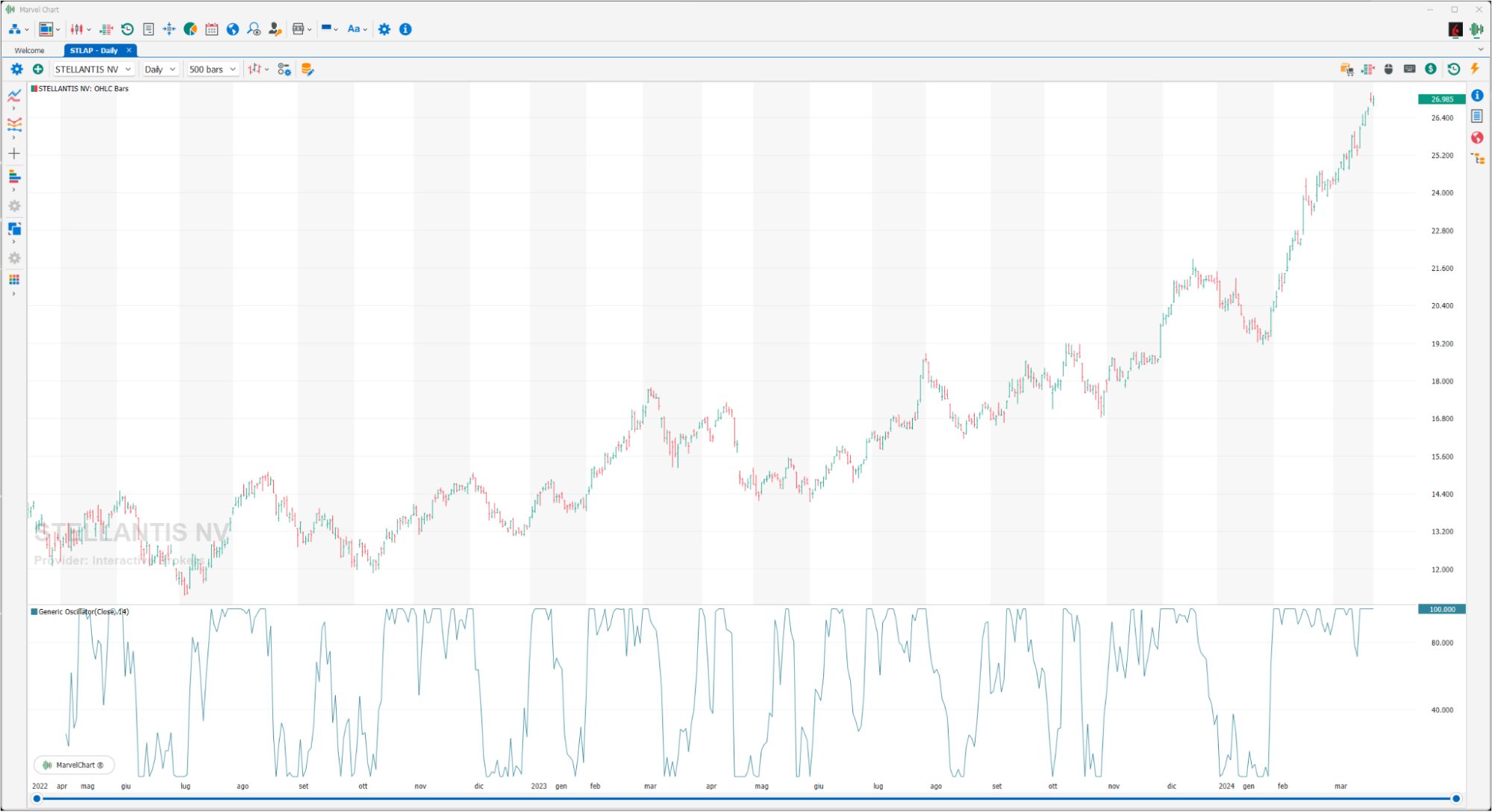
The Generic Oscillator is a function that translates the input price series into an oscillator between 0 and 100, using the LOW and high values in the period to scale and normalize the value of the current price.
Linear Regression Forecast
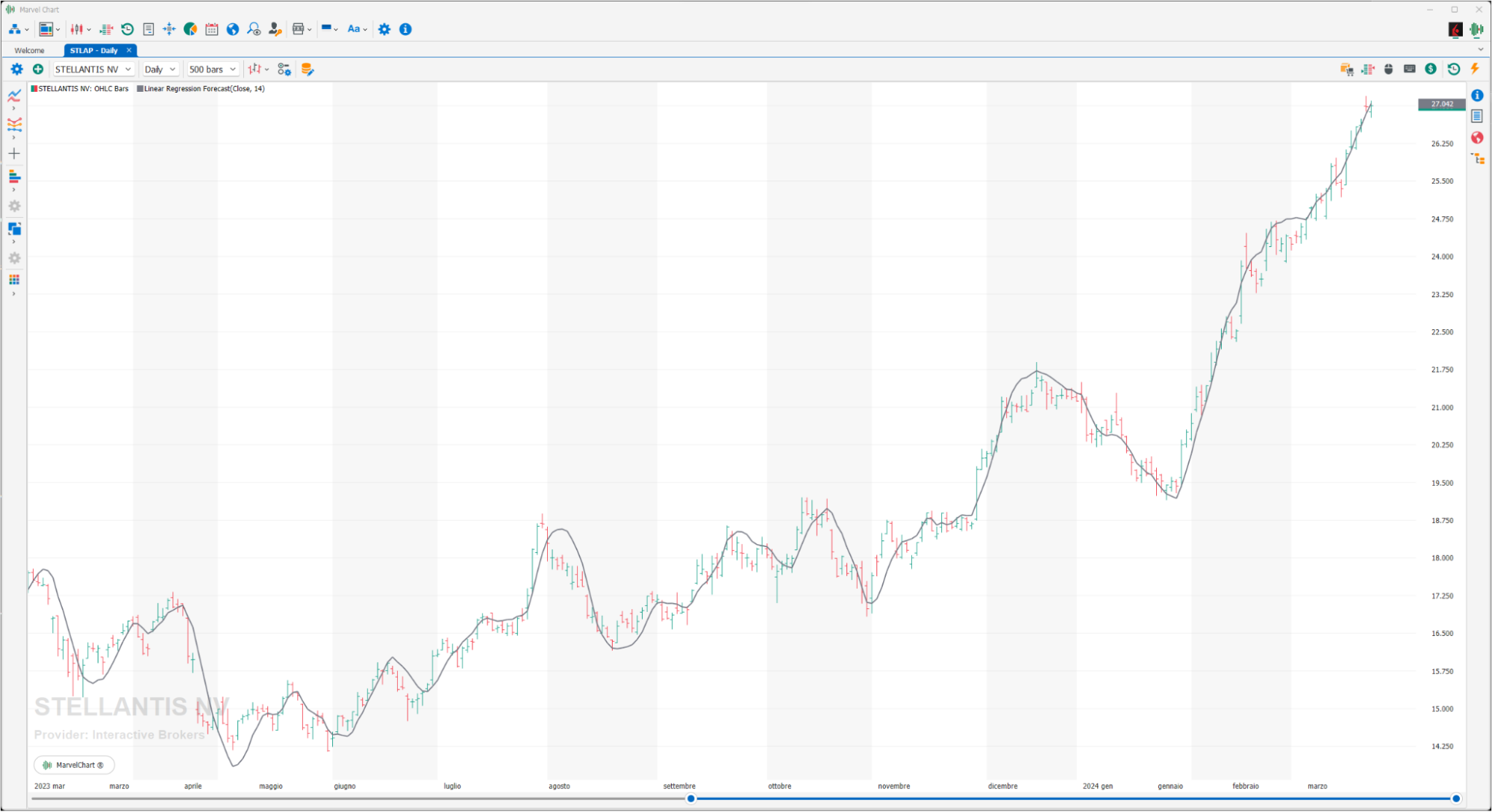
It is the simple linear regression, which is a method of finding the linear equation that best fits a set of data points. Linear regression forecasting tries to pass through multiple points while minimizing the distance between them. The interpretation of the linear regression forecast indicator is similar to the moving average but has the advantage of having a “lag”: since the indicator corresponds to a data line rather than an average, the linear regression forecast is more sensitive to price changes.
Linear Regression Intercept
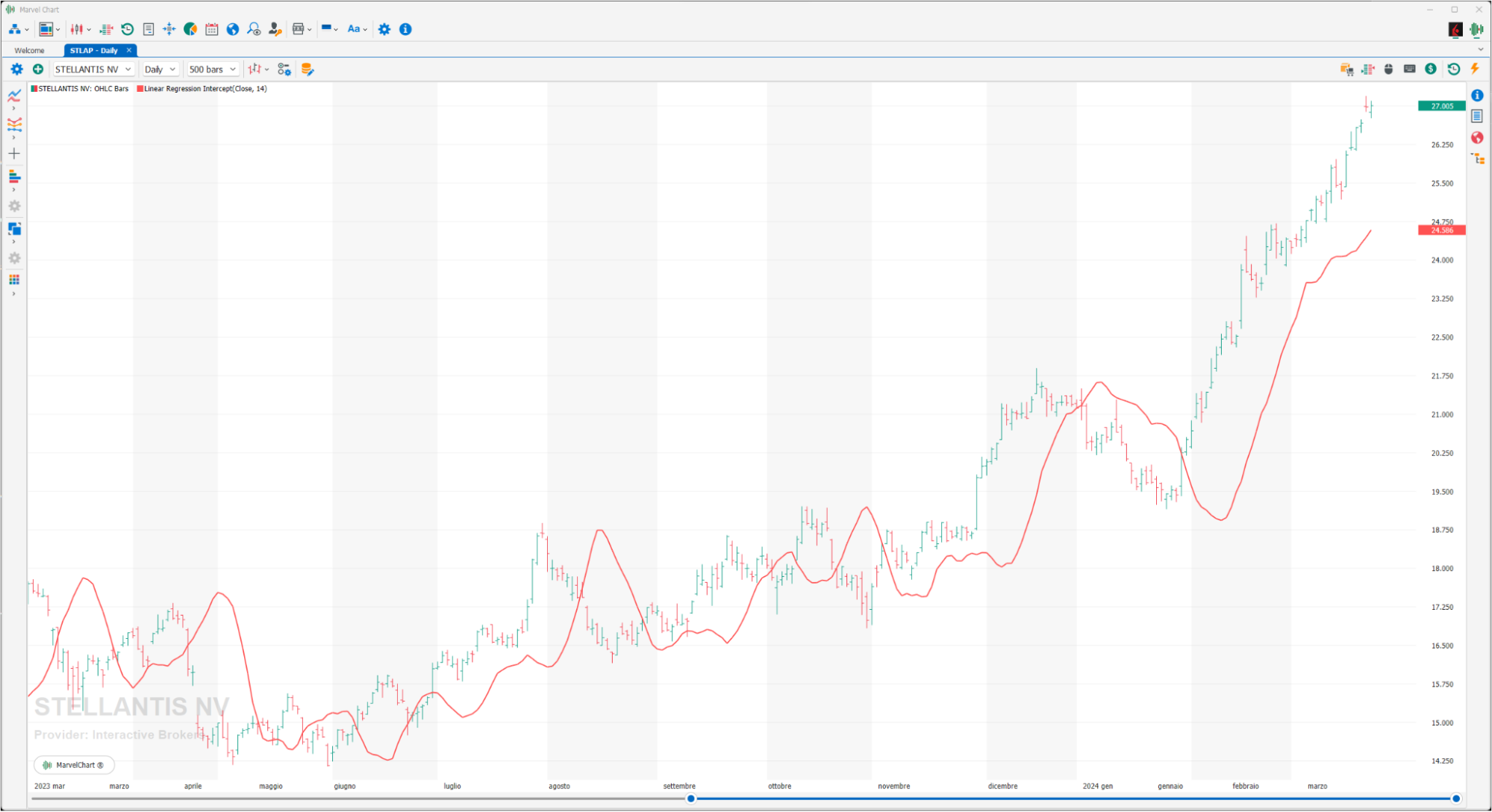
The Linear Regression Intercept is one of the statistical indicators calculated using linear regression, it is in fact calculated using the classic formula of the “Linear Regression Forecast” but assigning the Y value (price axis) assuming the X value (time axis) = 0.
Linear Regression R-Squared
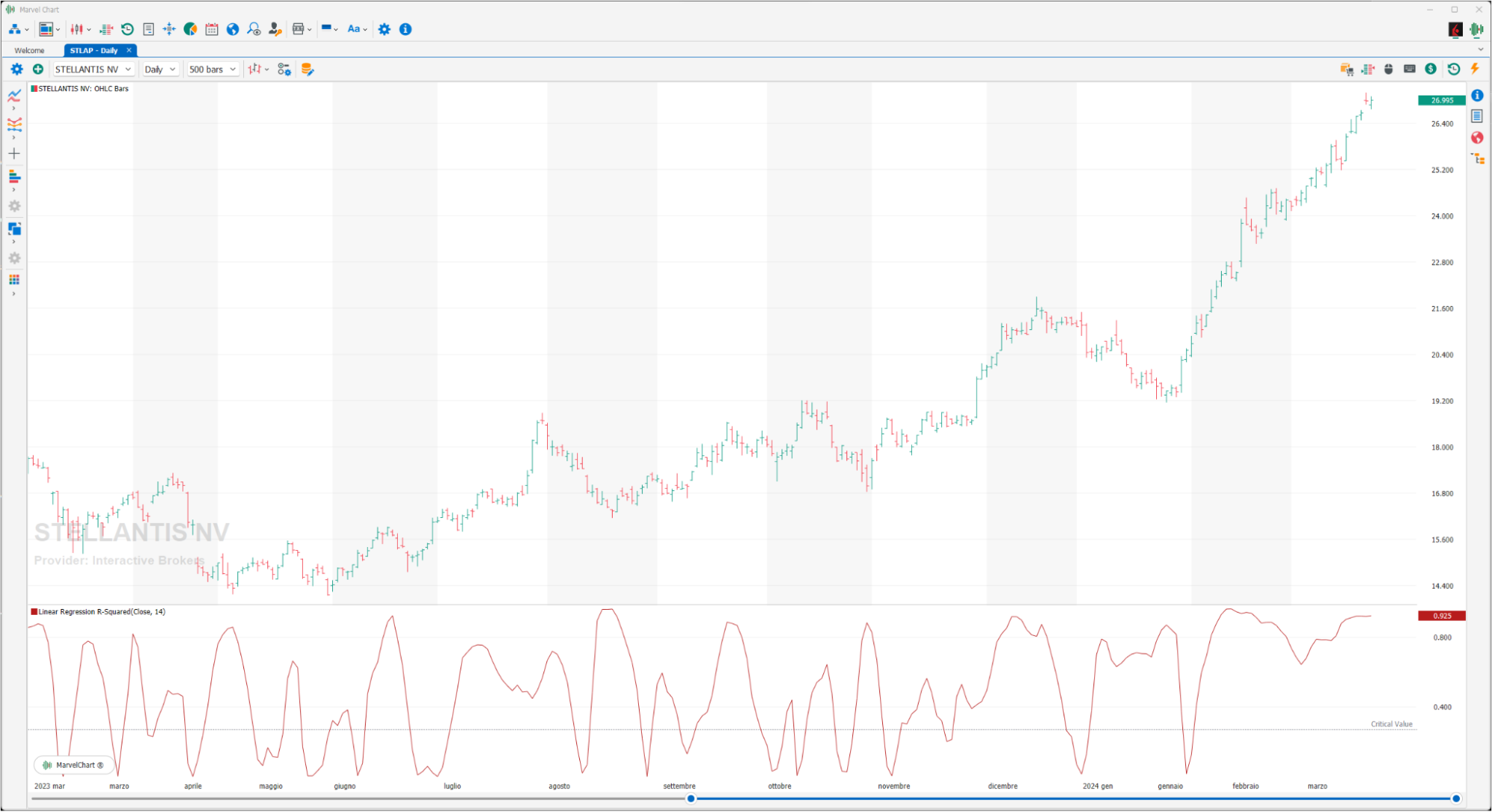
Linear regression is widely used by technical analysts. While the slope of the linear regression line indicates the direction of the market trend, r-squared highlights the strength of the market itself: the closer the prices are to the regression line, the stronger the trend. The value assumed by this variable identifies the percentage of price movement that is indicated by the linear regression, this means that a value equal to 0.3 (calculated over 21 periods) indicates that 30% of the price movement is included in the regression line, while the remaining 70% is not correlated with the linear regression. Low values express a high strength of the trend. To determine if the trend is statistically significant for a linear regression built on "x" periods, refer to the following table that shows the r-squared values required for a 95% confidence level, based on various time periods. If the value assumed by the indicator is lower than that indicated in the table, it must be deduced that prices do not show a statistically significant trend.
Periods | R-Squared value |
|---|---|
5 | 0.77 |
10 | 0.40 |
14 | 0.27 |
20 | 0.20 |
25 | 0.16 |
30 | 0.13 |
50 | 0.08 |
60 | 0.06 |
120 | 0.03 |
Linear Regression Slope
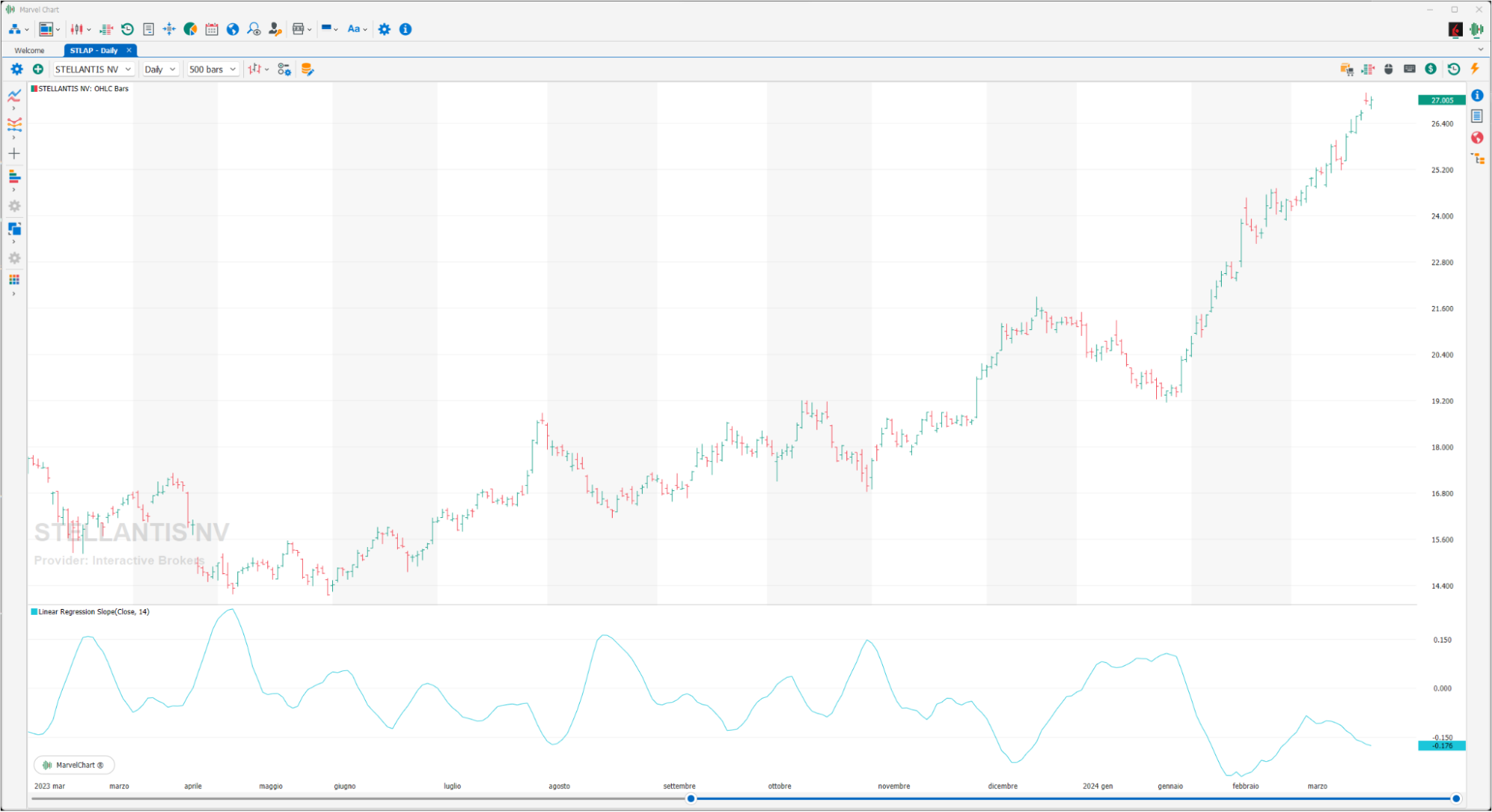
The Linear Regression Slope is an oscillator calculated using the linear regression technique. This technique is applied in technical analysis to determine whether the trend is bullish or bearish and with what intensity, considering past price fluctuations. As the name indicates, the slope of the linear regression, oscillates above and below the 0 line, is positive when the slope of the regression line (Slope) is greater than 0 and negative when it is less than 0. It can be used to measure the strength or weakness and direction of the trend.
Prime Number Oscillator
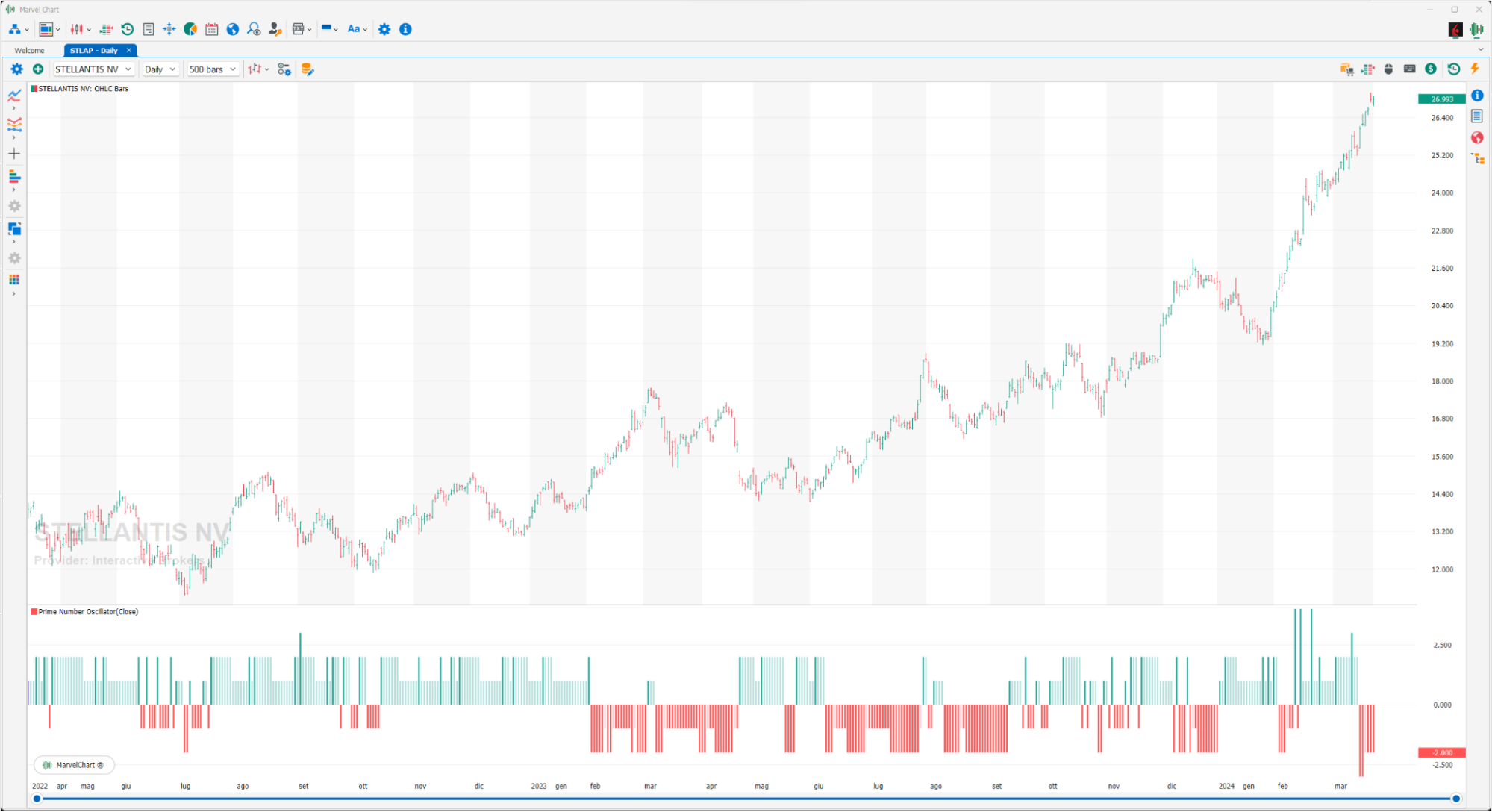
The Prime Number Oscillator is an indicator that is derived from the “Prime Number Bands” but displayed as an oscillator.
Rainbow Oscillator
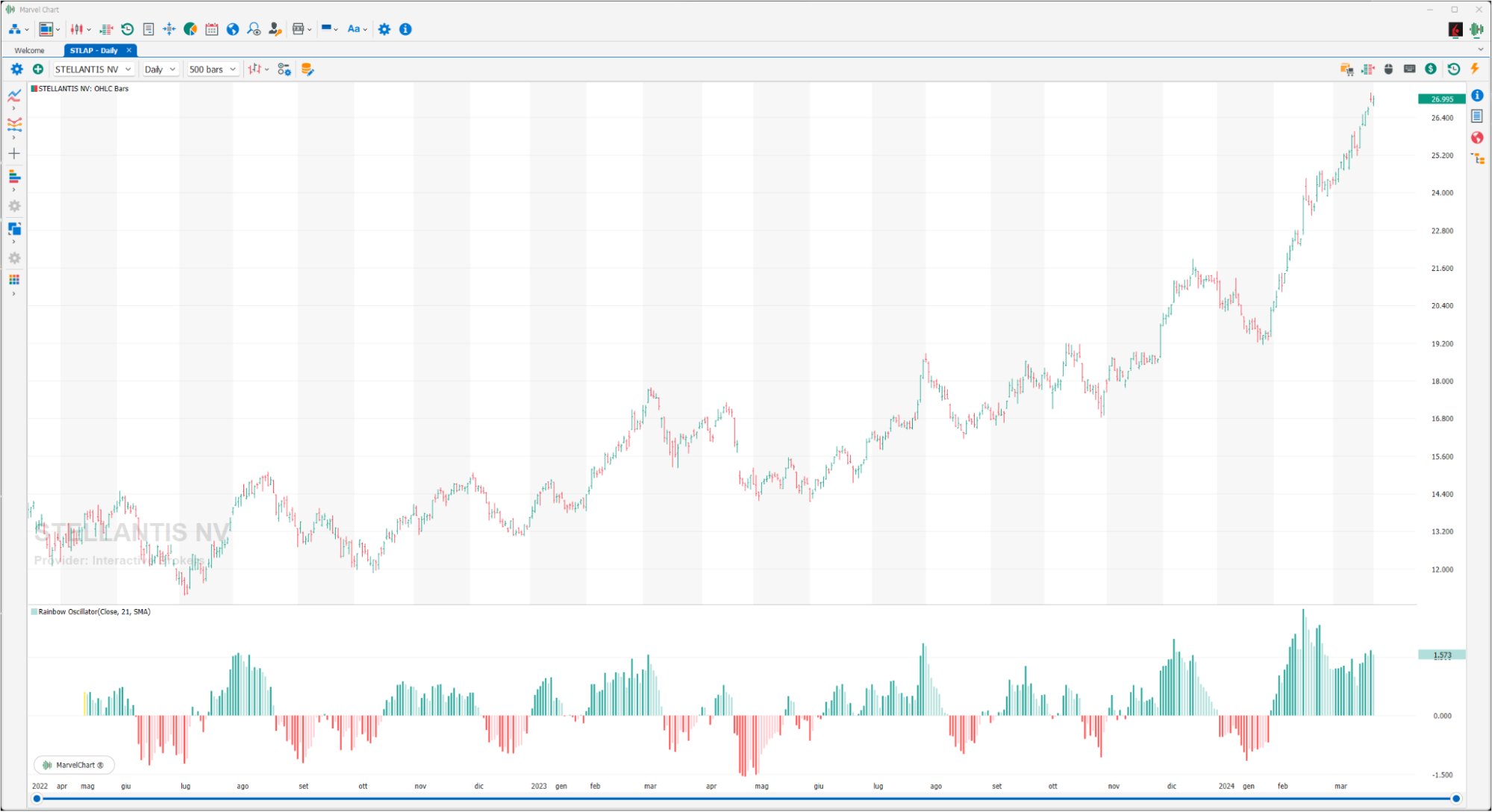
The Rainbow Oscillator indicator was created by Mel Widner in 1997. In essence, the indicator is calculated by averaging the difference between the price and the values of all “moving averages” with a period less than or equal to the value of the input Levels (it is recommended to display the Rainbow Oscillator as a histogram). The simple crossover indicates the potential change in trend; Rainbow Oscillator is a typical trend-following indicator and you will have to be careful, because in the lateral phases false signals will surely be generated. For this reason it can be more effective if used as a confirmation of price reductions from congested areas.
Random Walk Index
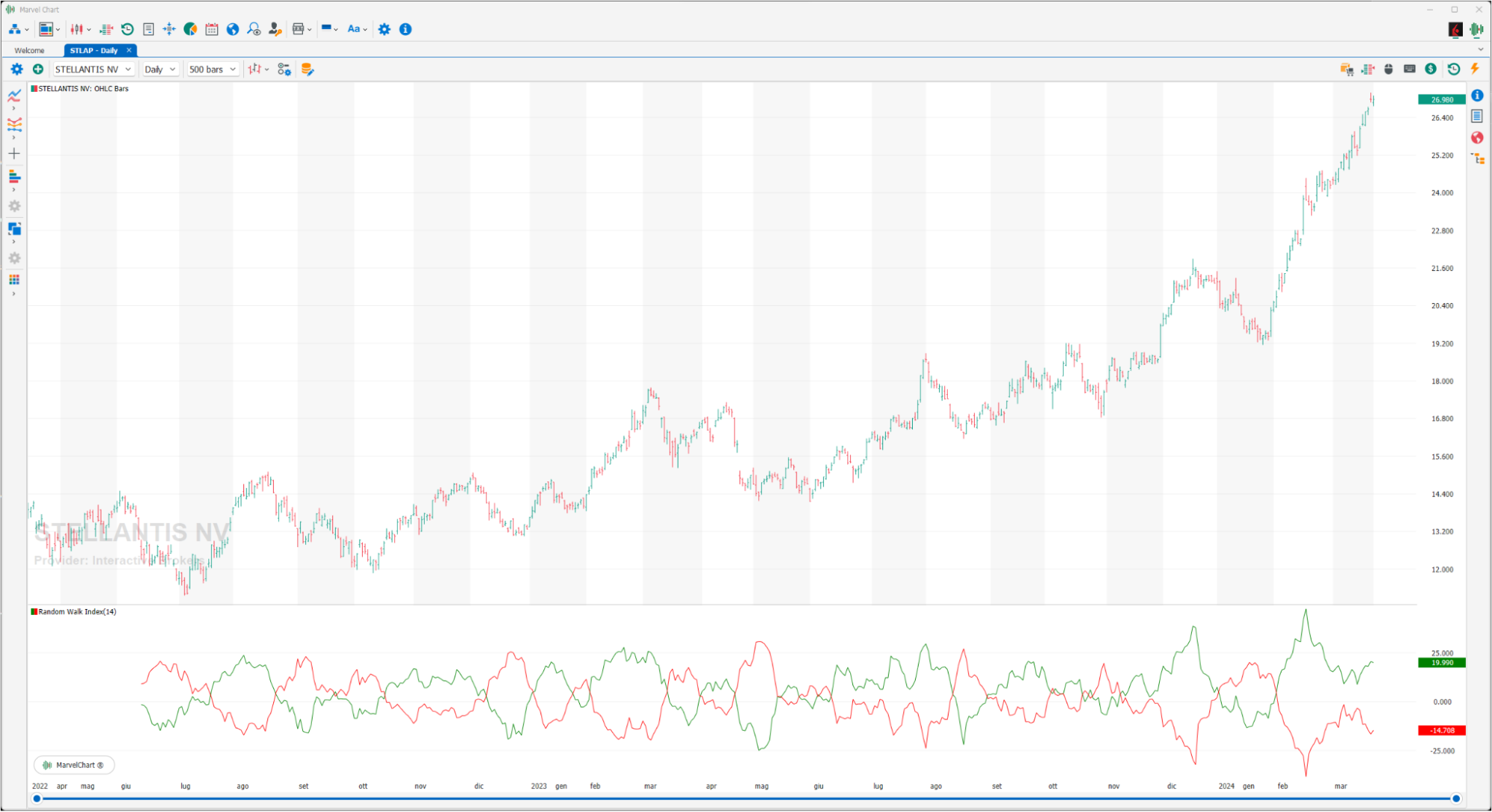
The Random Walk Index is an indicator that tries to determine whether the price movement of a financial instrument is random or the consequence of a statistically significant and therefore more reliable trend. The indicator is composed of two bands RWI High and RWI Low, the first identifies long trends, the second identifies short trends. The interpretation is very simple, the greater the width of the range between the two bands drawn, the greater the strength of the trend, long or short based on which of the two is above the 0 line.
Sine Wave
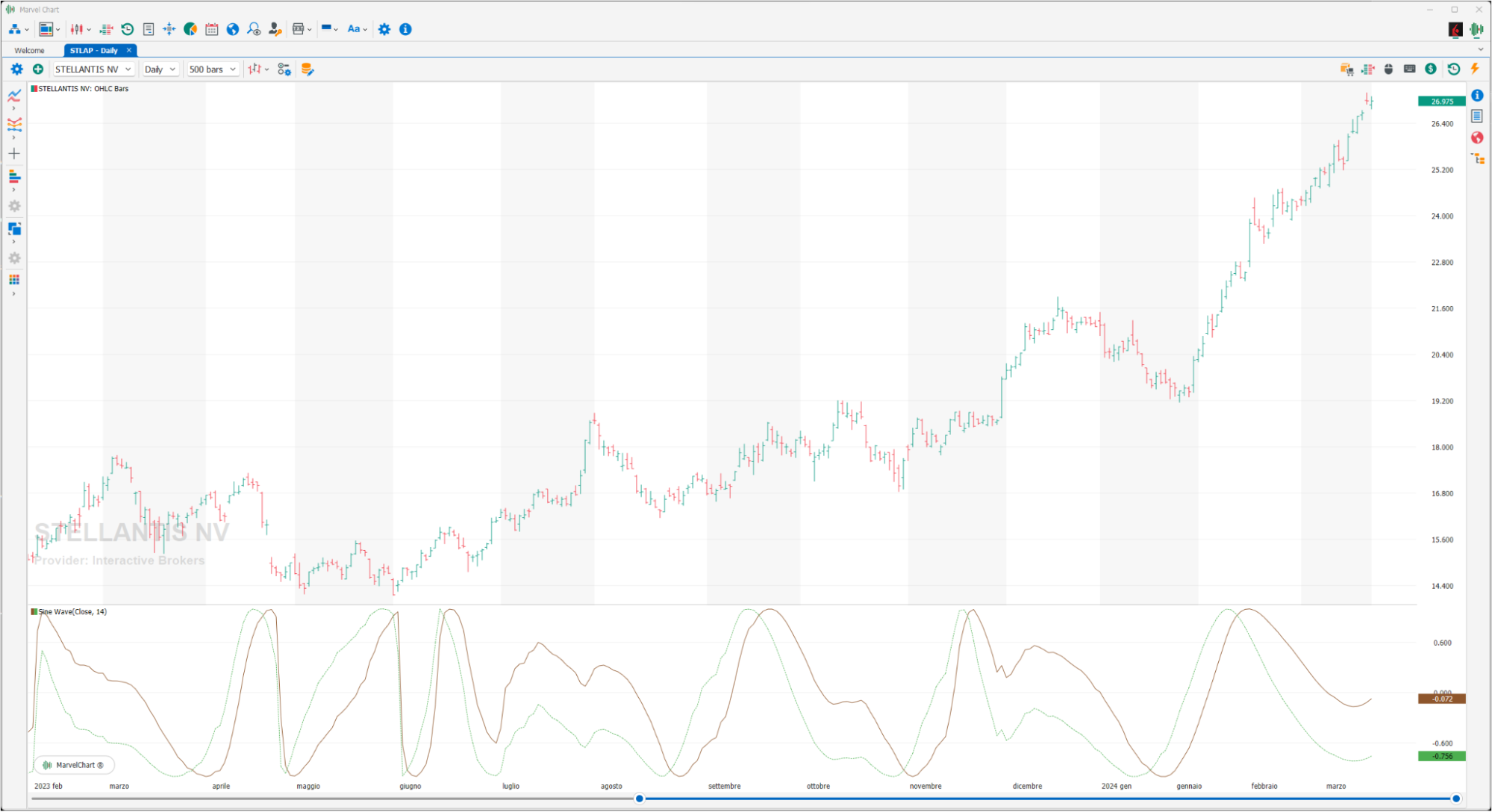
The Sine Wave is a recent indicator, created by John Ehlers in 1996 and used to highlight whether the stock is in a trend or in a cycle. The Sine Wave is composed of two graphs, the Sine Wave (green) and the Lead Sine (red), the first measures the phase, the second the phase increased by 45° degrees. Together the curves give indications on the state: in a defined trend or not in a trend. A BUY signal occurs when the Sine Wave (green) crosses the Lead Sine (red) at the top, a SELL signal when the Sine Wave (green) crosses the Lead Sine (red) at the bottom.
Standard Deviation
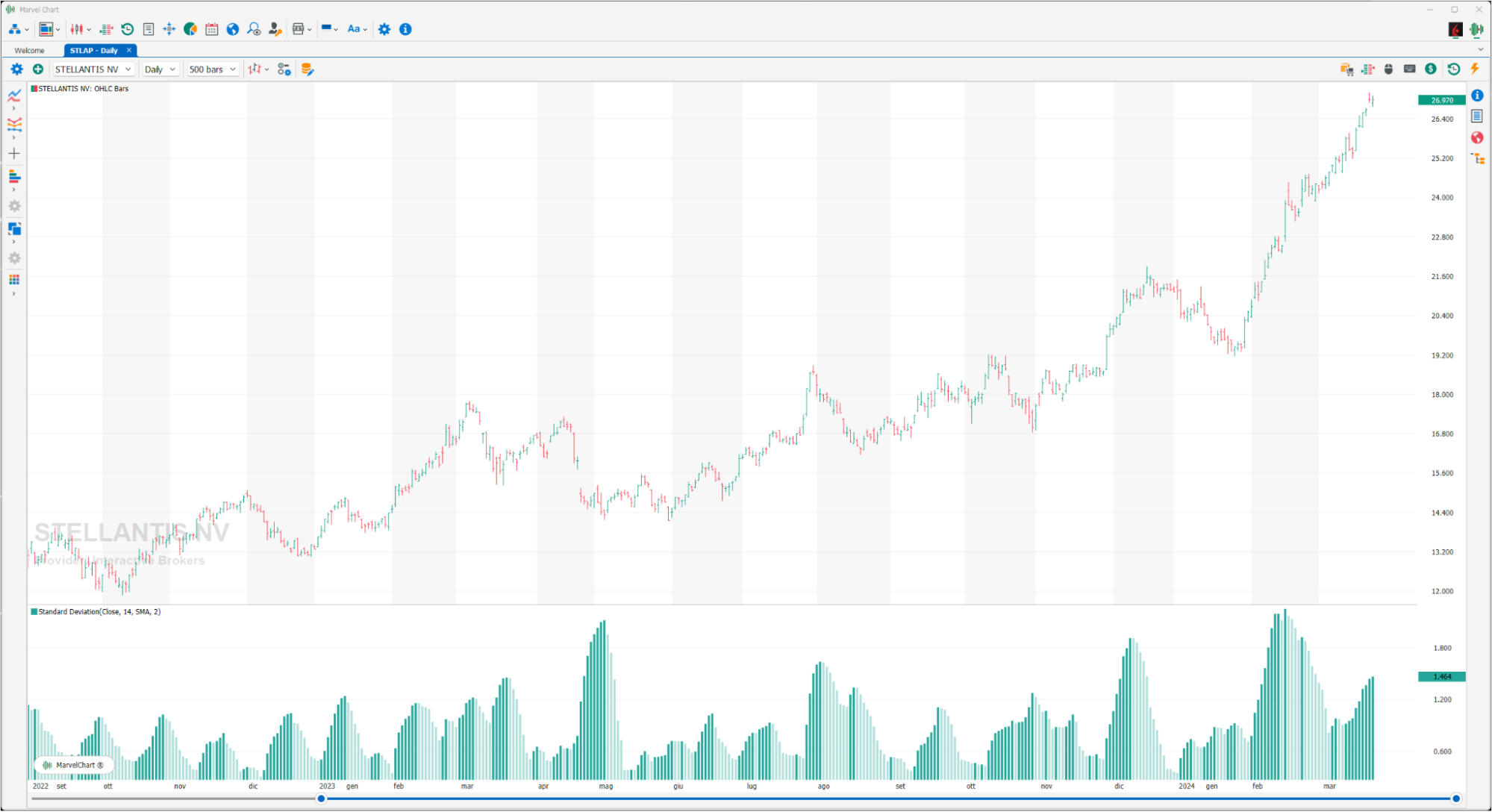
The standard deviation is an index that measures the volatility of prices, as the difference between average prices. It follows that the indicator will rise upwards when the difference between the current CLOSE price and the average CLOSE price is greater, and will fall in the opposite case. It can be used as a support to determine phases of euphoria or stability of the market: we will have peaks in the case of euphoria, while the values will be low in the presence of phases of laterality of the financial instrument being analyzed. Given the high number of information that often comes from other indicators, the Standard Deviation can be useful to have a general picture of the situation. The user can configure the indicator as he/she deems most appropriate, for example by applying it to OPEN prices, or by using other types of “Moving Averages”, or finally by changing the number of “Moving Averages” periods.
Standard Error
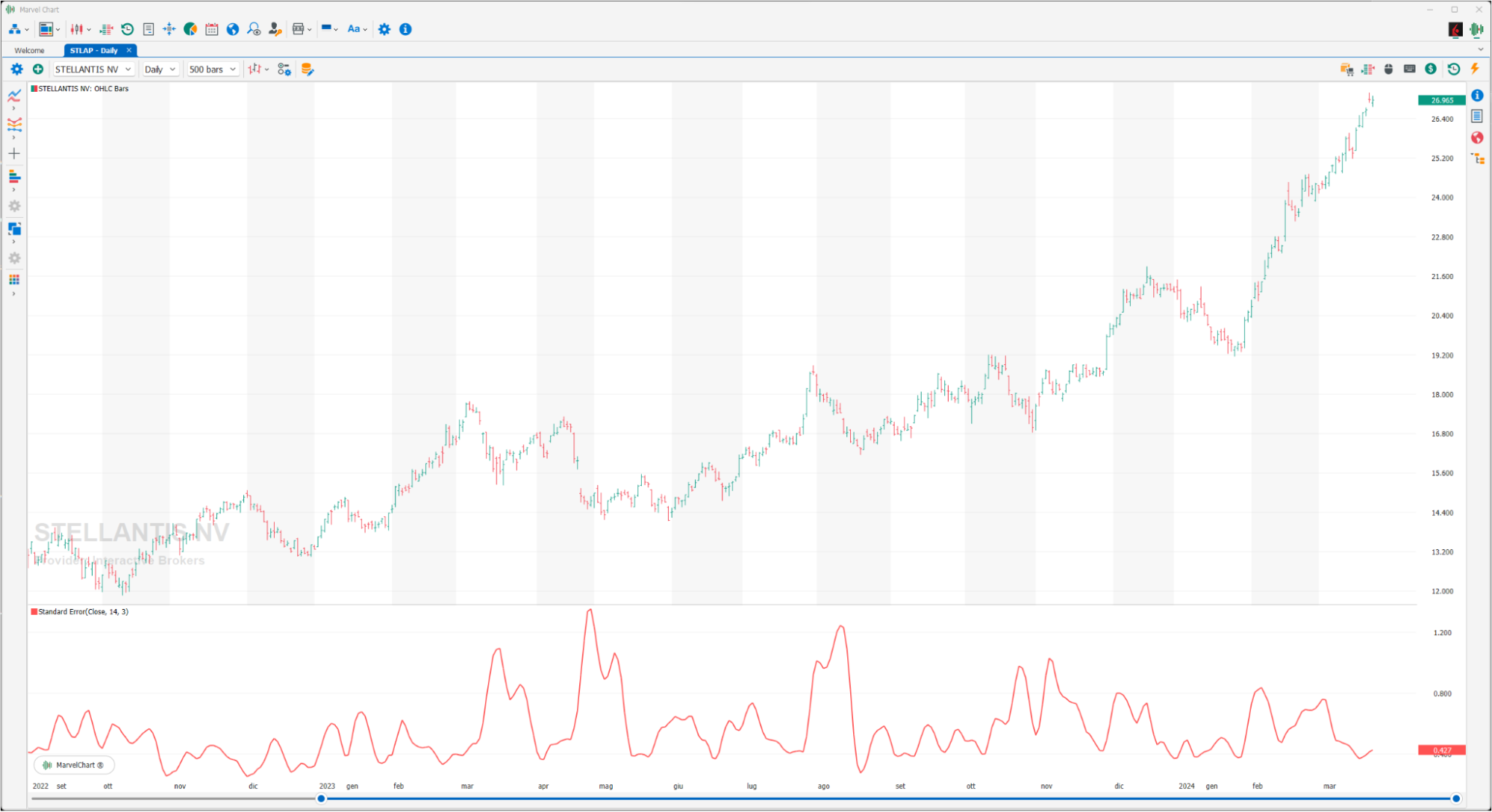
The Standard Error, for a specified period, measures how much the prices have deviated from a linear regression line for the same period. The higher the value, the more the prices have deviated from a linear regression line for the same period, while the lower the value, the closer the prices are to the linear regression line. If all the CLOSE prices were equal to the corresponding values of the linear regression line, the Standard Error would be zero.
Variance
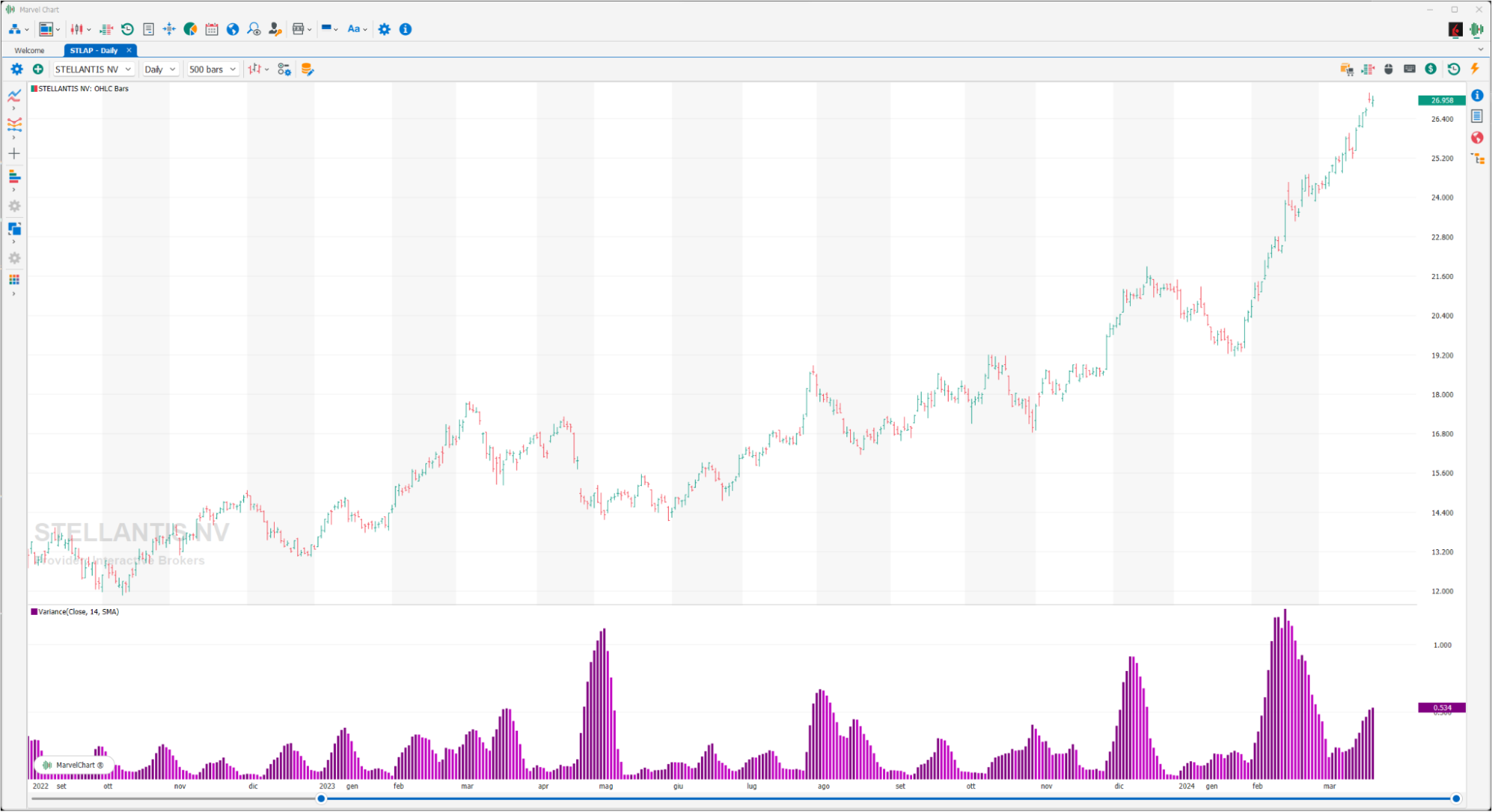
Given a series of values, it is the average of the squares of the deviations of the individual values from their arithmetic mean plotted in the histograms. For convenience, a color scale is assigned based on the price trend on which it is calculated.
Z-Score
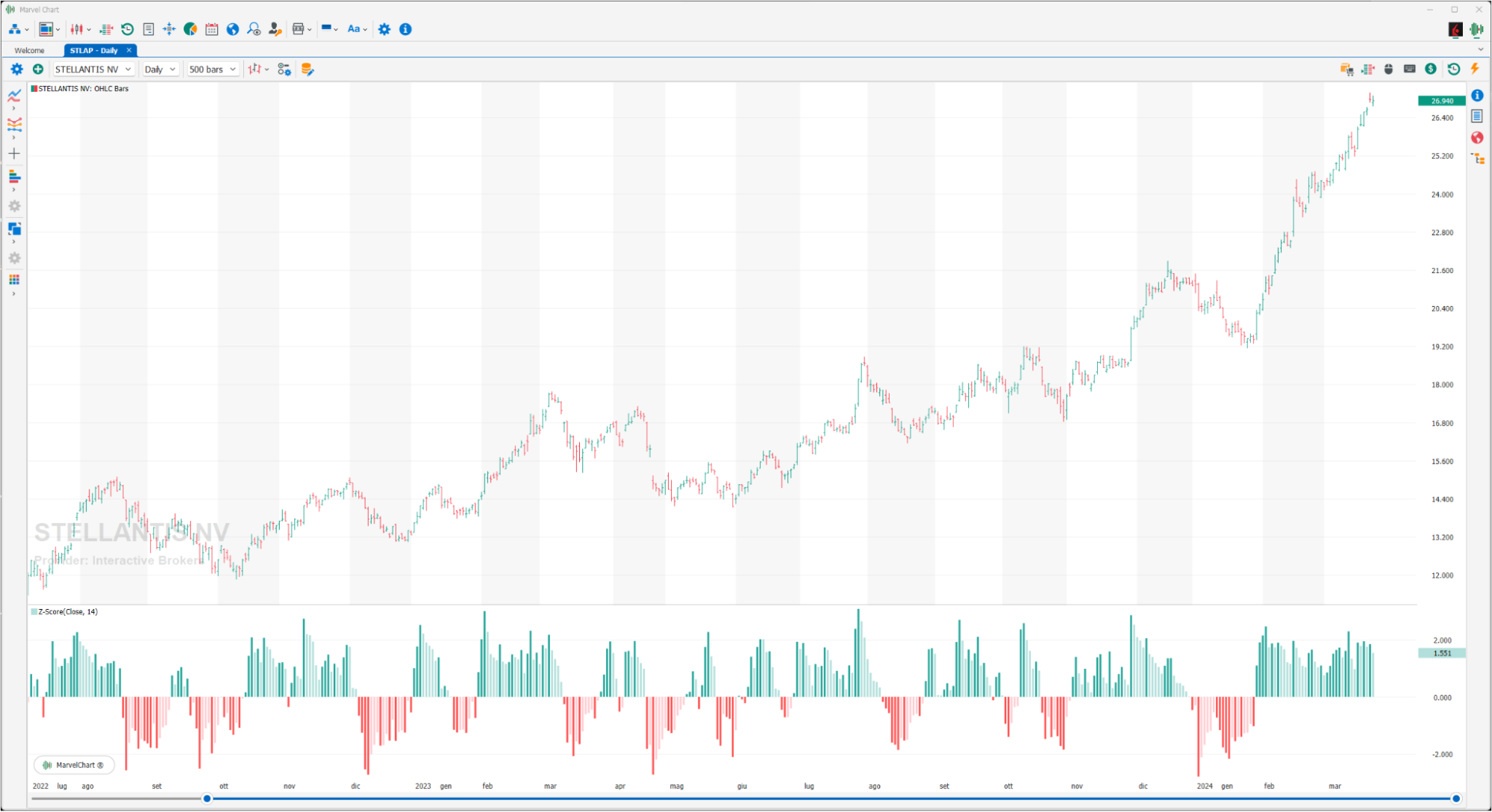
The Z-Score indicator can be used both on an asset chart and on a watchlist with a set of assets. The Z-Score represents the distance of a point in a data series from the mean of the same, expressed in number of standard deviations. Values greater than +2 indicate that there is a 95% probability that the values in the input vector will decrease. Values less than -2 indicate that there is a 95% chance that the values in the input vector will increase.